Wave processing
Attenuation correction
Measuring waves using a pressure transducer requires attenuation correction to the raw signal so that the actual wave signal at the surface could be correctly reflected (Figure 1). According to linear wave theories, this could be achieved by Discrete Fourier Transform (DFT), since all wave signals could be considered as a composition of waves with different frequencies, and we can treat each frequency component separately (Figure 2).

Figure 1. Example to illustrate wave signal attenuated with depth (Wiki (1)).
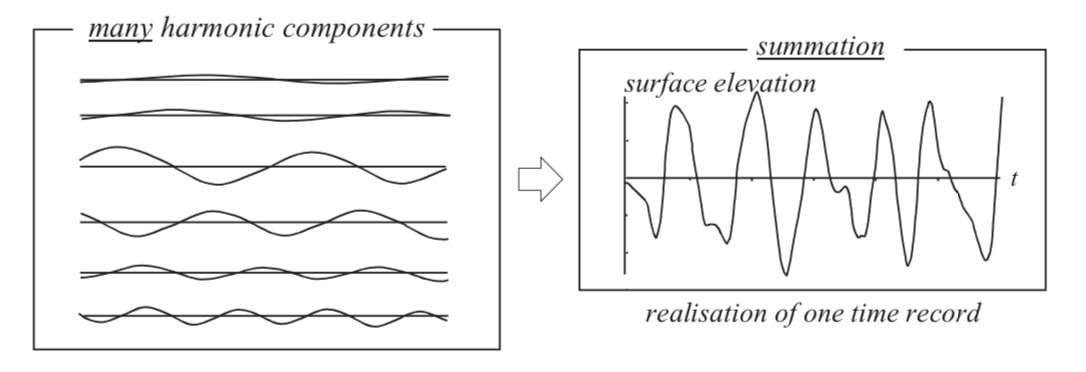
Figure 2. Any realization of time record could be considered
as the summation of many frequency components (Holthuijsen (2)).
The attenuation correction includes three major steps (Gibbons (3)).
Transform time-series data to its frequency domain.
Multiply each frequency by the inverse of the attenuation by that particular frequency due to the depth of the instrument. This action is limited to attenuation <1/20 to avoid injecting noise into the reconstruction.

3. Transform the corrected frequency back to the time domain using the inverse Fourier transform .
Windowing
When applying the Fourier Transform to time series data, the underlying assumption is that the two endpoints of a time waveform are connected together and if an integer number of periods fill the acquisition time interval, the transform turns out fine. However, in reality, this could never be the case. When the measured signal is not an integer number of periods, the endpoints are discontinuous. The artificial discontinuities appear as high-frequency components not present in the original signal after DFT. This is known as spectral leakage. To minimize the effect, the windowing technique is introduced (Figure 3). There are many different types of window functions that could be applied depending on the signal. In general, the Hann window is satisfactory in 95 percent of cases. Ruskin applies a 96-point Hann window to the first 48 and the last 48 samples of each burst before DFT. Once the frequency signal after attenuation correction is transformed back to the time domain, the head and tail of the wave height time series previously affected by the Hann window will not be transformed by an inverse Hann window, but are simply excluded from the wave statistics calculation.
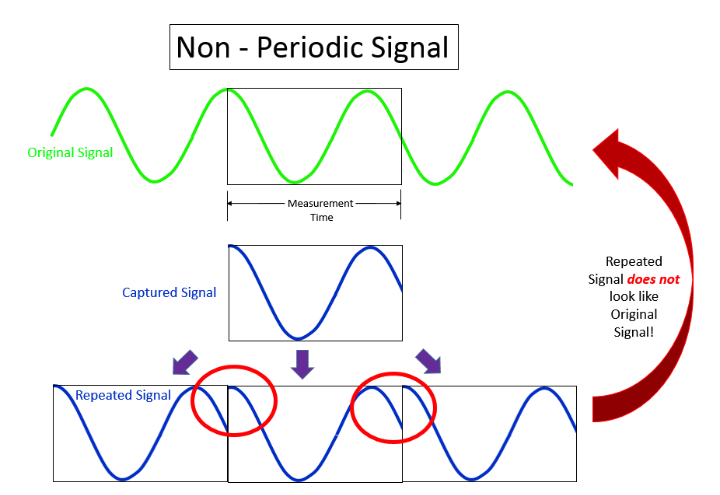
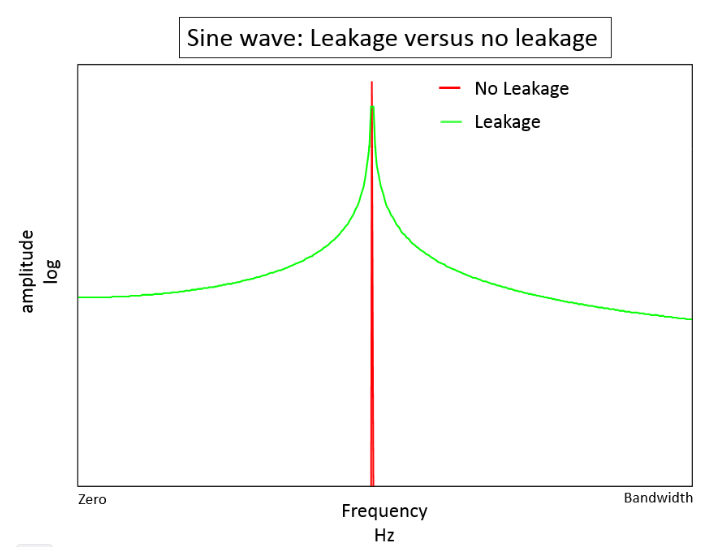
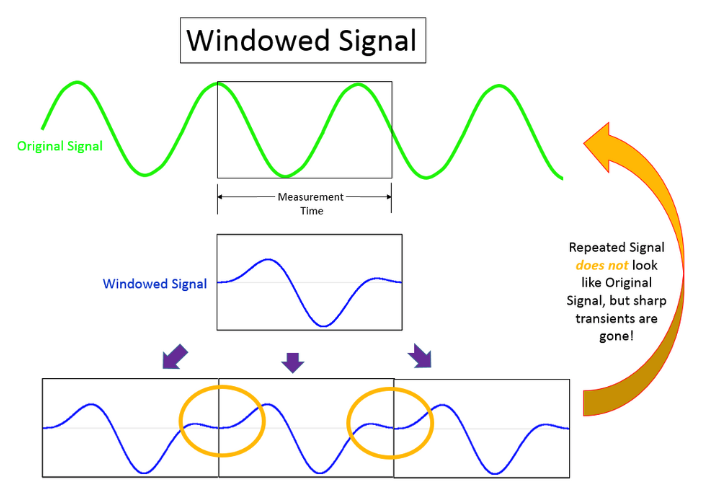
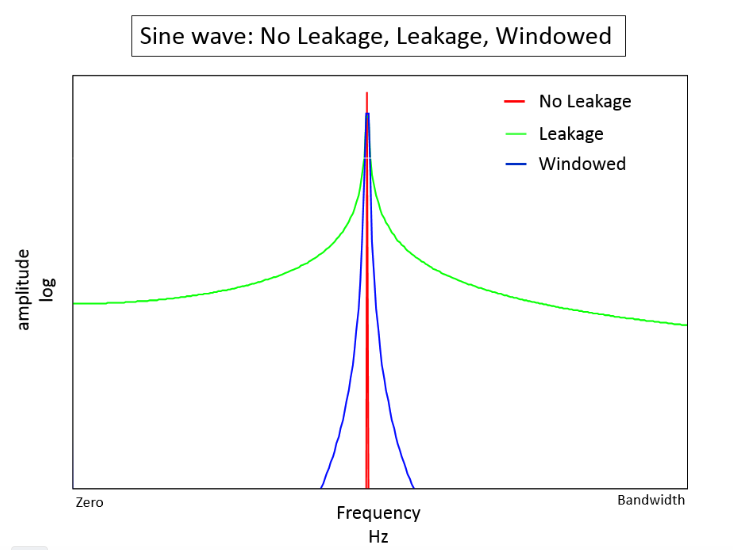
Figure 4. Example to illustrate how windowing minimizes spectral leakage (Siemens (5)).
Procedures implemented in Ruskin software
Transforming the data
Find the linear regression of the burst data.
Find the “mean depth”, which is the depth at the middle of the burst calculated by the linear regression.
Remove mean depth and detrend the burst data.
Apply a Hann window on the burst data (window size 96 samples) to provide hdata.
Apply a 1D real-only DFT on hdata to provide fdata.
Find max frequency in fdata, which is either the largest frequency or the largest frequency that can be detected without aliasing (Nyquist).
Remove frequencies higher than max frequency and conjugate aliases in fdata.
Apply attenuation-correction to each frequency in fdata.
Determine principle frequency.
IDFT fdata to provide ihdata.
Calculating the statistics based on ihdata
Exclude the head and tail (total 96 samples) of the wave time series.
Calculate variance (see Mobley (6)).
Calculate energy = variance * gravity * density * 1000.0.
Default gravity = 9.80665m/s2
Default density = 1.0281kg/m3Determine negative-to-positive zero crossings in time domain, ignoring the first partial wave (and dropping the last partial wave).
Calculate average period = sum(periods) / n.
Calculate average height = sum(heights) / n.
Rank sort waves by height.
Determine max height and max period.
Calculate significant height and period on the largest 1/3 of the waves.
Calculate 1/10 height and period on the largest 1/10 of the waves.
References
Image. https://en.wikipedia.org/wiki/Wind_wave (accessed Feb 17, 2022).
Holthuijsen, Leo H., Waves in Oceanic and Coastal Waters, 2007. Waves-in-Oceanic-and-Coastal-Waters (accessed Feb 17, 2022).
Gibbons, D. T., G. Jones, E. Siegel, A. Hay, and F. Johnson, Performance of a new submersible Tide-Wave recorder, Oceans, 2005. Proceedings of MTS/IEEE, vol. 2, pp. 1057–1060, IEEE, New York, doi:10.1109/OCEANS.2005.1639895 Performance of a new submersible Tide-Wave recorder (accessed Feb 17, 2022).
Earle, M. D. Nondirectional and Directional Wave Data Analysis Procedures; NDBC Technical Document 96-01, Slidell, Louisiana; 1996. Nondirectional and Directional Wave Data Analysis Procedures (accessed Feb 17, 2022).
Siemens/Testing, Windows and Spectral Leakage. https://community.plm.automation.siemens.com/t5/Testing-Knowledge-Base/Windows-and-Spectral-Leakage/ta-p/432760 (accessed Feb 17, 2022).
Mobley, C. Wave Energy. wave-variance-spectra-theory (accessed Feb 17, 2022).
