Wave parameters

These are the parameters that Ruskin calculates for the wave processing computation: 

1.    Significant wave height/period: average height and period of the largest 1/3 of the waves in the burst.

2.    1/10 wave height/period: average height and period of the largest 1/10 of the waves in the burst.

3.    Maximum wave height/period: the wave in the burst period with the greatest height and period respectively.

4.    Average wave height/period: the sum of the heights and period divided by the number of samples in the burst.

5.    Wave energy: the average energy of the waves in the burst.

Below shows the breakdown of wave distribution defined by the parameters above.

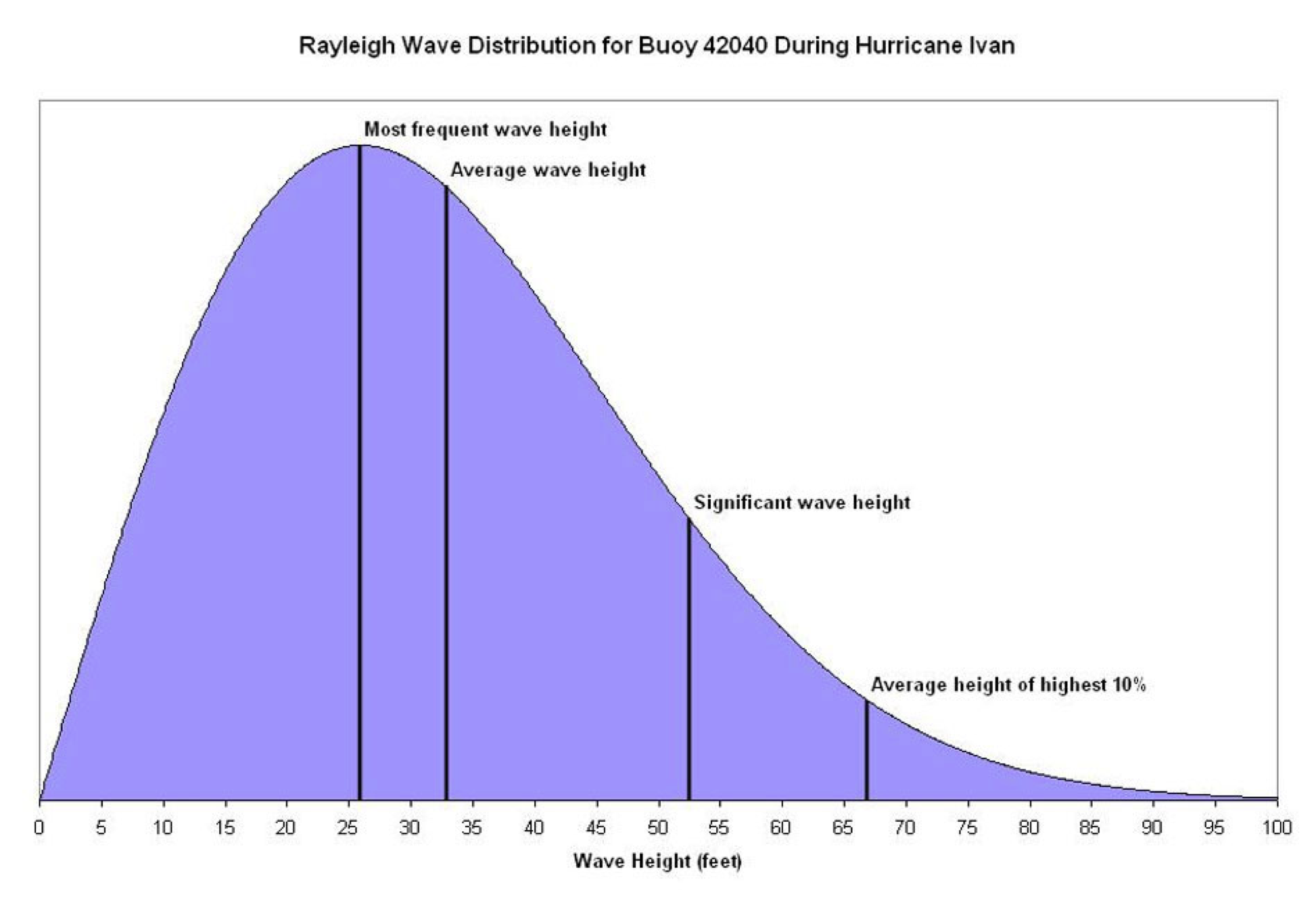
Figure 2. Parameters that define the wave distribution.

Tidal slope

The tidal slope is calculated using a 15-sample window centered around the point of interest. The values are weighted with Discrete Fourier Transform (DFT) coefficients and averaged over a window function.

Wave burst

The n-samples in the burst are linearly detrended, using a least-squares linear regression, and centered around the mean. The values are then scaled with a 96-sample Hanning Window. The DFT of the resulting values is taken and from the output, only the real values are kept. If the mean depth is greater than 0, out of range frequencies are removed. The values are corrected to surface values. The spatial wave is restored with an inverse discrete Fourier transform (IDFT), and scaling removed by an inverse 96-sample Hanning Window.

Wave energy

Variance is the average over one wavelength of the surface elevation squared.

The first (partial) wave is ignored for averaging purposes, though it is counted for the variance and wave energy.

Significant wave height and period

The average of the first 3rd of the wave height/period values sorted in descending order of height.

The average height of the highest 10%

The average of the first 10th of the wave height/period values sorted in descending order of height.

References: 

(1)       Earle, M. D. Nondirectional and Directional Wave Data Analysis Procedures; NDBC Technical Document 96-01, Slidell, Louisiana; 1996.

(2)       Gibbons, D. T., G. Jones, E. Siegel, A. Hay, and F. Johnson (2005), Performance of a new submersible Tide-Wave recorder, Oceans, 2005. Proceedings of MTS/IEEE, vol. 2, pp. 1057–1060, IEEE, New York, doi:10.1109/OCEANS.2005.1639895.

(3)       Mobley, C. Wave Energy http://www.oceanopticsbook.info/view/surfaces/level_2/wave_variance_spectra__theory (accessed Apr 21, 2017).